前缀和

前缀和作用：快速求出元素组中某段区间的和

一维前缀和

原数组: a[1], a[2], a[3], a[4], a[5], …, a[n]

前缀和 S[i] 为数组的前 i 项和

前缀和: S[i] = a[1] + a[2] + a[3] + … + a[i]

for循环求出 每个S[i], 将 S[0] 定义为 0，便于处理边界问题

求 [l, r]中的和, 即为 S[r] - S[l-1]

二维前缀和

s[i][j] 为以（1，1）为左上角，以（i, j) 为右下角的子矩阵的所有元素之和

则有：s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j]

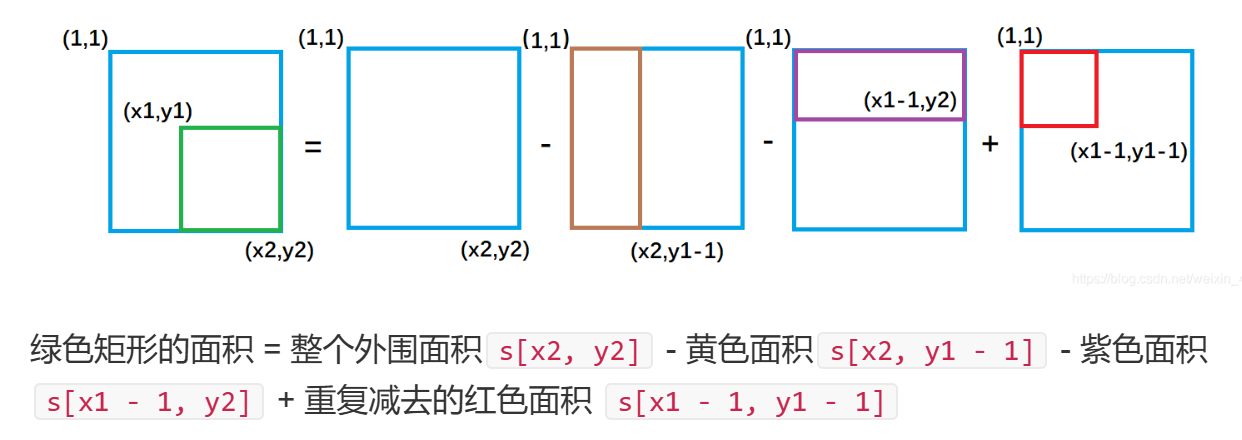
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的所有元素之和为：
sum = s[x2][y2] - s[x1 - 1][y2] - s[x2] [y1 - 1] + s[x1 - 1][y1 - 1]

差分

差分作用：快速对元素组中某段区间进行加减操作

一维差分

原数组 a：a[1], a[2], a[3], ..., a[n];

差分数组 b：b[1], b[2], b[3], ..., b[i];

其中 b[i] = a[i] - a[i - 1];

则有 a[i] = b[1] + b[2] + b[3] + ... + b[i]
图示：

给区间 [l, r] 每个元素加上 c, 即为：b[l] += c, b[r + 1] -= c;

二维差分

若原数组为 n 行，m 列
因为 原数组 为 差分数组 的 前缀和数组
所以，b[x][y] += c,
则表示原数组 以 （x, y) 为左上角，以 (n, m) 为右小角的子矩阵所有元素都加上 c

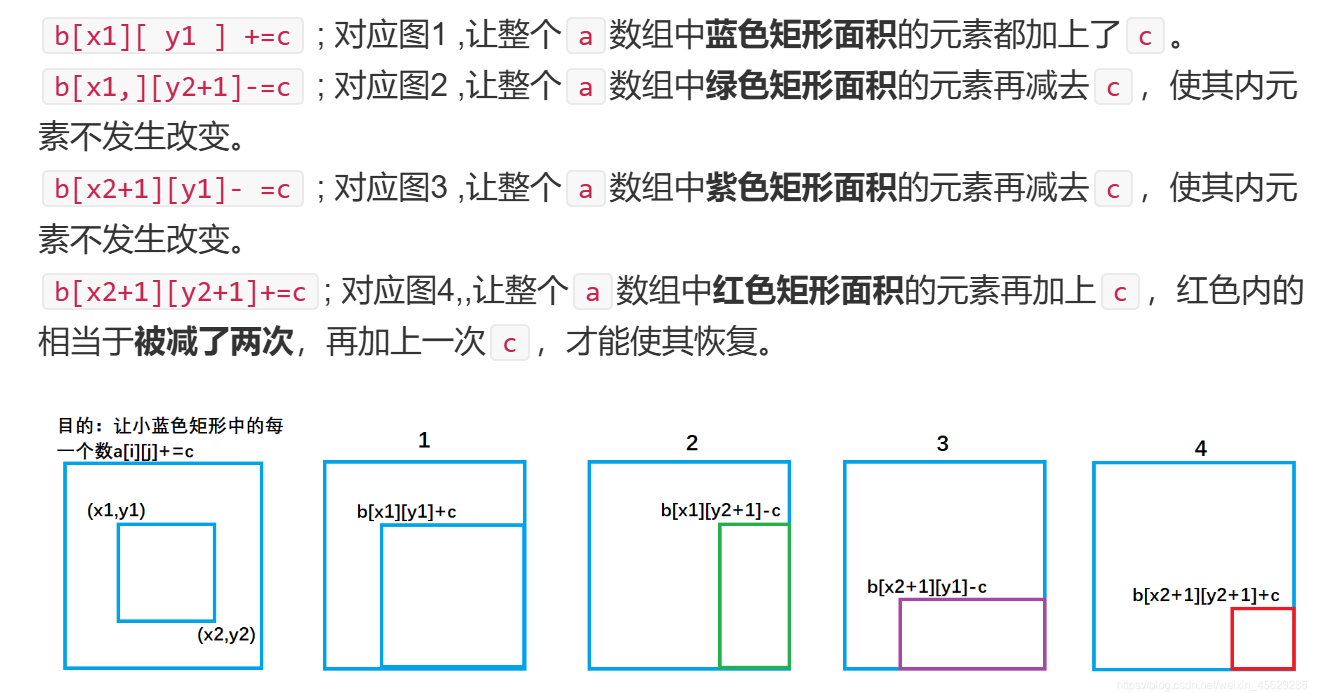
// 以 (x1, y1) 为左上角，以 (x2, y2) 为右下角的子矩阵所有元素都加上 c
void insert(int x1,int y1,int x2,int y2,int c)
{     //对b数组执行插入操作，等价于对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了c
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}

例题
输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c 。

请你将进行完所有操作后的矩阵输出。

#include<bits/stdc++.h>
using namespace std;

int main() {
    int n, m, q;
    cin >> n >> m >> q;

    vector<vector<int>> d(n + 2, vector<int>(m + 2, 0));

    auto add = [&](int x1, int y1, int x2, int y2, int c) {
        d[x1][y1] += c;
        d[x1][y2 + 1] -= c;
        d[x2 + 1][y1] -= c;
        d[x2 + 1][y2 + 1] += c;
    };

    for (int i = 1; i <= n; ++ i) {
        for (int j = 1; j <= m; ++ j) {
            int t;
            cin >> t;
            add(i, j, i, j, t);
        }
    }

    while (q --) {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        add(x1, y1, x2, y2, c);
    }

    for (int i = 1; i <= n; ++ i) {
        for (int j = 1; j <= m; ++ j) {
            d[i][j] += d[i - 1][j] + d[i][j - 1] - d[i - 1][j - 1];
            cout << d[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}