The 2022 ICPC Asia Xian/Jinan Regional Contest\2022 ICPC 亚洲区域赛西安站和济南站题解记录
|
313
|
0
|
🎓 理工

西安站题解（B, C, E, F, G, J, L）

西安站补题链接

B. Cells Coloring

题意

给定一个 n x m 的网格，有一些格子有障碍，其余格子为空。

选定一个整数 k，使用 0，1，... k 共 k 种颜色对无障碍格子进行染色，并满足同行或同列不能有相同的非 0 颜色。

假设 0 颜色的个数为 z, 给定两个数 c, d。
求最小化 ck + dz 的值

解法

图论（网络流）

可以发现，若某行某列最大的（非 0）有色格子的数量为 x, 则 k = x 时，满足同行同列不能有相同的非 0 颜色的条件。

设 tot 为所有无障碍格子的数量
设 zt 为染成非 0 色的格子的数量
则 z = tot - zt
原式转为 ck + d * (tot - zt)

可以考虑枚举 k 值，使每行每列染的非 0 有色格子数不超过 k 的情况。

可以发现，原式子最小化即为，在固定 k 值的情况下最大化 zt 的值。

可以这样建图 {

抽出一个 “行点”， 这个行的 “行点” 向这一行
的每一个点连接一条容量为 1 的边

从 源点 向每一行的 “行点” 连接一条容量为 k 的边

抽出一个 “列点”，这个列的 “列点” 向这一列的每一个点连接一条容量为 1 的边

每一列的 “列点” 向 汇点 连接一条容量为 k 的边。
}

可知该图上跑出的最大流极为 zt 值

这里最大流使用的是 Dinic 算法，时间复杂度不好估计，但如果每次都重新建图跑一遍最大流必然会超时。

这里有个小优化，顺序枚举 k 值，在残量网络上增加 源点 到 “行点”， “列点” 到 汇点 之间所有边的容量即可

代码

#include<bits/stdc++.h>
#define forn(a, b, c) for (int i = b; i < c; ++ i)
#define INF 0x3f3f3f3f
using namespace std;
#define endl '\n'
#define ll long long

const int N = 1e5 + 5, M = 1e6 + 5;
int h[N], e[M], ne[M], f[M], idx;
int q[M], cur[N], d[N]; // cur 当前弧优化
ll n, m, S, T, c, dk;
void add(int a, int b, int c){
    e[idx] = b;
    ne[idx] = h[a];
    f[idx] = c;
    h[a] = idx ++;
}

bool bfs() {
    forn(i, 0, N) d[i] = -1;
    int hh = 0, tt = 0;
    q[tt ++] = S;
    d[S] = 0;
    cur[S] = h[S];
    while (hh < tt) {
        int t = q[hh ++];
        for (int i = h[t]; i != -1; i = ne[i]) {
            int ver = e[i];
            if (d[ver] == -1 && f[i]) {
                d[ver] = d[t] + 1;
                cur[ver] = h[ver];
                if (ver == T) return true;
                q[tt ++] = ver;
            }
        }
    }
    return false;
}

int find(int u, int limit) {
    if (u == T) return limit;
    int flow = 0;

    for (int i = cur[u]; i != -1 && flow < limit; i = ne[i]) {
        int ver = e[i];
        cur[u] = i;
        if (d[ver] == d[u] + 1 && f[i]) {
            int t = find(ver, min(f[i], limit - flow));
            if (!t) d[ver] = -1;
            f[i] -= t, f[i ^ 1] += t, flow += t;
        }

    }
    return flow;
}

int dinic() {
    int r = 0, flow = 0;
    while (bfs()) while (flow = find(S, INF)) r += flow;
    return r;
}

void solve() {

    cin >> n >> m >> c >> dk;
//  cout << n << " " << m << " " << c << " " << dk << endl;
    S = N - 1, T = N - 2;
    int tot = 0;
    memset(h, -1, sizeof h); 
    for (int i = 0; i < n; ++ i) {
        string s;
        cin >> s;

        int row = n * m + i;
        int col = n * m + n;
        for (int j = 0; j < m; ++ j) {
            int cur = i * m + j;

            if (s[j] == '.') {
                ++ tot;

                add(row, cur, 1);
                add(cur, row, 0);

                add(cur, col + j, 1);
                add(col + j, cur, 0);
            }
        }
    }

    ll ans = 1e18;
    ll rt = 0;

    for (int i = 0; i < n; ++ i) {
        int row = n * m + i;
        add(S, row, 0);
        add(row, S, 0);
    }

    for (int j = 0; j < m; ++ j) {
        int col = n * m + n + j;
        add(col, T, 0);
        add(T, col, 0);
    }

    for (int k = 0; k <= max(n, m); ++ k) {

        if (k)
            for (int i = h[S]; i != -1; i = ne[i]) {
                f[i] ++;
            }

        if (k)
            for (int i = h[T]; i != -1; i = ne[i]) {
                f[i - 1] ++;
            }

        rt += dinic();
        int z = tot - rt;
        ans = min(ans, c * k + dk * z);
    }

    cout << ans << endl;

}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int T = 1;
//  cin >> T;

    while (T--) {
        solve();
    }

    return 0;
}

C. Clone Ranran

题意

Ranran 要解决 c 个问题

他有两种操作：

1.花 a 分钟复制一个自己

2.花 b 分钟解决一个问题

复制出来的自己同样能执行这两种操作

问解决 c 个问题所需的最小的时间

解法

枚举 / 贪心

可知，最优做法一定是先复制完自己，再一起解决问题

因为问题的总数最大为$10^{9}$，复制自己的次数最多为 31 次

可以枚举复制的次数，取结果最小值

代码

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
const int N = 5E4 + 10;

ll qmi(ll a, int k) {
    ll ans = 1;
    while (k) {
        if (k & 1) ans = ans * a;
        a = a * a;
        k >>= 1; 
    }
    return ans;
}
void solve() {

    ll a, b, c;
    cin >> a >> b >> c;
    ll ret = 1e18 + 5;
    for (int i = 0; i <= 32; ++ i) {
        ll t = a * i + ((c + qmi(2, i) - 1) / qmi(2, i)) * b;
        ret = min(ret, t);
    }
    cout << ret << endl;

}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int T = 1;
    cin >> T;

    while (T --) {
        solve(); 
    } 

    return 0;
}

E. Find Maximum

题意

file

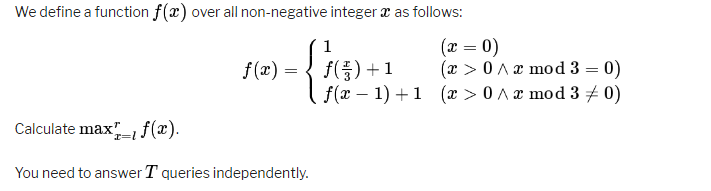
解法

三进制 / 构造

可以 f(x) 值即为 x 的三进制数上每一位数的和加上三进制长度，例如 14 的三进制为 112 则 f(14) = 1 + 1 + 2 + 3 = 7

给定 l 和 r 的区间找最大的 f(x) 值， l <= x <= r

进行如下构造，以 r 为上界，进行三进制分解，从高位到低位遍历，高位减去一个 1 则后面所有低位都可以变成 2, 不难发现这样一定可以找到最优解

代码

#include <iostream>
#include <utility>
#include <algorithm>
#include <vector>

using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;

const int N = 1e5 + 10;

ll f(ll x) {
    if (x == 0) return 1;
    if (x == 1) return 2;
    if (x == 2) return 3;
    if (x == 3) return 3;
    return (x % 3) + 1 + f(x / 3);
}

int main() {

    ios::sync_with_stdio(false);

    int t;
    cin >> t;
    while(t --) {

        ll l, r;
        cin >> l >> r;

        if(l == r) {
            cout << f(r) << endl;
            continue;
        }

        ll _r = r;
        vector<int> rbit;
        while(_r) {
            rbit.push_back(_r % 3);
            _r /= 3;
        }

        ll ans = max(f(l), f(r));
        reverse(rbit.begin(), rbit.end());

        for(int i = 0; i < (int)rbit.size(); i ++) {

            if(rbit[i] == 0) continue;

            ll p = 0;

            // 高位减 1，低位都变 2
            for(int j = 0; j < i; j ++) p = p * 3 + rbit[j];

            p = p * 3 + rbit[i] - 1;

            for(int j = i + 1; j < (int)rbit.size(); j ++) p = p * 3 + 2;

            if(p >= l) ans = max(ans, f(p));
        }
        cout << ans << '\n';
    }

    return 0;
}

F. Hotel

题意
略

解法

贪心
略

代码

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
const int N = 5E4 + 10;

void solve() {
    int n, c1, c2;
    cin >> n >> c1 >> c2;
    vector<string> arr; 
    for (int i = 0; i < n; ++ i) {
        string s;
        cin >> s;
        arr.push_back(s);
    }

    if (c2 >= c1 * 2) {
        cout << 3 * n * c1 << endl;
        return;
    }

    int b1 = 0, b2 = 0;
    for (string& s : arr) {
        if (s[0] == s[1] || s[1] == s[2] || s[0] == s[2]) {
            ++ b2;
            if (c2 < c1) ++ b2;
            else ++ b1;
        }else {
            if (c2 < c1) b2 += 3;
            else b1 += 3;
        }
    }
    cout << b1 * c1 + b2 * c2 << endl;

}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int T = 1;
//  cin >> T;

    while (T --) {
        solve(); 
    } 

    return 0;
}

G. Perfect Word

题意

给定 n 个字符串

找到最长的一个完美字符串，其所有子串都在给定的字符串里

解法

方法一：

二分

可以发现
1.完美字符串一定在给定的字符串里
2.完美字符串的长度是符合单调性的，即可二分完美字符串的长度，暴力匹配

方法二：

Trie 树

建立一个字典树，即可在线性的时间内判断一个字符串是否是完美字符串，对每一个给定的字符串进行判断，取合法的最长的

代码

方法一

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
const int N = 5E4 + 10;

void solve() {
    map<int, set<string>> mp;

    int n;
    cin >> n;
    for (int i = 0; i < n; ++ i) {
        string t;
        cin >> t;
        if (t.size() > 320) continue;
        int k = t.size();
        mp[k].insert(t); 
    }
//  for (int i = 1; i <= 2; ++ i) {
//      for (string s : mp[i]) cout << s << " ";
//      cout << endl;
//  } 
    auto check = [&](int u) {

        for (string s : mp[u]) {

            int f = 1;
            for (int len = 1; len <= s.size(); ++ len) {
                for (int i = 0; i + len - 1 < s.size(); ++ i) {
                    if (!mp[len].count(s.substr(i, len))) {
                        f = 0;
                        break;
                    }
                }
            } 
            if (f) return true;
        }   
        return false;
    };

    int l = 1, r = 321;
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid)) {
            l = mid + 1;
        }else r = mid; 
    }
    cout << -- l << endl;

}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int T = 1;
//  cin >> T;

    while (T --) {
        solve(); 
    } 

    return 0;
}

J. Strange Sum

题意

略

解法

a 为最大数，b 为次大数

答案为 max{0, a, a + b}

代码

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
const int N = 5E4 + 10;

void solve() {
    int n;
    cin >> n;
    vector<int> arr;
    for (int i = 0; i < n; ++ i) {
        int v;
        cin >> v;
        arr.push_back(v);
    }
    sort(arr.begin(), arr.end());
    int ret = 0;

    if (arr.back() > 0) ret += arr.back();
    if (arr[arr.size() - 2] > 0) ret += arr[arr.size() - 2];

    cout << ret << endl; 

}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int T = 1;
//  cin >> T;

    while (T --) {
        solve(); 
    } 

    return 0;
}

L. Tree

题意

给定一个 n 个节点的树，将树进行子集划分

每个子集至少满足以下其中一个要求

1.任意两个节点 u, v，u 和 v 存在祖先关系
2.任意两个节点 u, v, u 和 v 不存在祖先关系

解法

思维

具体结合代码和画图模拟过程理解

d[i] 为深度为 i 的节点个数，叶子节点深度为 1

可以看成从叶子节点往上

原来叶子节点深度为 1

每次删去最外层叶子节点 + 下一层每个节点作为链起点

选最小值

代码

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
const int N = 5E4 + 10;

void solve() {

    int n;
    cin >> n;
    vector<vector<int>> e(n + 1);
    vector<int> d(n + 5);

    for (int i = 2; i <= n; ++ i) {
        int p;
        cin >> p;
        e[p].push_back(i);
    }
    int mx = 0;
    function<int(int u)> dfs = [&](int u) ->int {
        int ans = 0;
        for (int j : e[u]) {
            ans = max(ans, dfs(j));
        }
        ++ ans;
        mx = max(mx, ans);
        d[ans] ++;
        return ans;
    };

    dfs(1);
    int ans = d[1];
//  cout << mx << endl;
    for (int i = 0; i <= mx; ++ i) {
        ans = min(ans, i + d[i + 1]);
    }

    cout << ans << endl;

}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int T = 1;
    cin >> T;

    while (T --) {
        solve(); 
    } 

    return 0;
}

济南站题解（A，D，E，K，M）

济南站补题链接

A. Tower

题意

有 n 座不同高度的塔

有以下三种操作

1.选择一座塔，将塔的高度增加 1
2.选择一座塔，将塔的高度减少 1
3.选择一座塔，将塔的高度调整为原高度一半

可以任选 m 座塔去除，问去除塔后，使剩下所有塔高度一致的最少操作次数

题解

模拟 / 暴力

枚举所有塔，枚举以当前塔为基准，所有最少操作次数

最后取个最小值

代码

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
const int N = 5E4 + 10;

void solve() {
    int n, m;
    cin >> n >> m;
    vector<int> arr;
    for (int i = 0; i < n; ++ i) {
        int x;
        cin >> x;
        arr.push_back(x);
    }
    ll ans = 1e18;
    for (int i = 0; i < n; ++ i) {
        int target = arr[i];
        while (target) {
            priority_queue<int, vector<int>, less<int>> q;

            for (int j = 0; j < n; ++ j) {
                if (arr[j] <= target) q.push(target - arr[j]);
                else if (arr[j] > target) {
                    int t = arr[j];
                    int anst = 0;
                    while (abs(t - target) > abs((int)t / 2 - target)) {
                        t /= 2;
                        ++ anst;
                    }
                    anst += abs(t - target);
                    q.push(anst);
                }
            }
            for (int i = 0; i < m && q.size(); ++ i) {
                q.pop();
            }
            ll anst = 0;
            while (q.size()) {
                anst += q.top();
                q.pop();
            }
            ans = min(ans, anst);
            target /= 2;
        }

    }
    cout << ans << endl;
}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int T = 1;
    cin >> T;

    while (T --) {
        solve(); 
    } 

    return 0;
}

D. Frozen Scoreboard

题意

规则就是 ICPC 规则

给定一支队伍的提交情况，和 最终结果（过题数 和 罚时数）

问 提交情况 和 最终结果 是否能匹配

若能则 Yes 和任意一种方案

否则输出 No

解法

回溯 / 模拟

最多就 13 个题，回溯过题情况，计算最少需要罚时和最大罚时

若最终罚时落在该区间，即当前情况可用，注意细节部分即可

代码

#include<bits/stdc++.h>

using namespace std;
//#define endl '\n'
#define ll long long
const int N = 15;
struct asdf {
    int x, y, id;
    char opt;
} a[N], b[N];
int n, m, ft, ac, tot, use[N];
char ch;

bool dfs(int t, int num, int l, int r) {
    if (num == ac) {
        if (!((l <= ft) && (ft <= r))) return 0;
        while (t <= tot) use[t++] = 0;
        return 1;
    }
    if (num > ac) return 0;
    if (tot - t + 1 + num < ac) return 0;
    use[t] = 1;
    if (dfs(t + 1, num + 1, l + (b[t].y - b[t].x) * 20 + 240, r + (b[t].y - 1) * 20 + 299)) return 1;
    use[t] = 0;
    return dfs(t + 1, num, l, r);
}

bool check() {
    if (ac < 0 || ft < 0 || ac > tot) return 0;
    return (dfs(1, 0, 0, 0));
}

void print() {
    cout << "Yes" << endl;
    for (int i = 1; i <= tot; ++i)
        if (use[i]) {
            a[b[i].id].opt = '+';
            a[b[i].id].y = (b[i].y - b[i].x) * 20 + 240;
            ft -= (b[i].y - b[i].x) * 20 + 240;
        } else a[b[i].id].opt = '-', a[b[i].id].x = b[i].y;
    for (int i = 1; i <= tot; ++i) {
        if (!use[i]) continue;
        a[b[i].id].y += min(ft, (b[i].x - 1) * 20 + 59);
        ft -= min(ft, (b[i].x - 1) * 20 + 59);
        a[b[i].id].x = min(((a[b[i].id].y - 240) / 20), b[i].y - 1) + 1;
        a[b[i].id].y -= (a[b[i].id].x - 1) * 20;
    }
    for (int i = 1; i <= m; ++i) {
        printf("%c ", a[i].opt);
        if (a[i].opt == '-') printf("%d", a[i].x);
        if (a[i].opt == '+') printf("%d/%d", a[i].x, a[i].y);
        printf("\n");
    }

}

void solve() {
    cin >> n >> m;
    while (n--) {
        tot = 0;
        cin >> ac >> ft;
        for (int i = 1; i <= m; ++i) {
            cin >> a[i].opt;
            a[i].id = i;
            if (a[i].opt == '+') {
                scanf("%d/%d", &a[i].x, &a[i].y);
                ac--;
                ft -= a[i].y;
                ft -= (a[i].x - 1) * 20;
            }
            if (a[i].opt == '?') scanf("%d%d", &a[i].x, &a[i].y), b[++tot] = a[i];
            if (a[i].opt == '-') scanf("%d", &a[i].x);
        }
        if (check()) print();
        else cout << "No" << endl;;

    }
}

int main() {
//  ios_base::sync_with_stdio(0);
//  cin.tie(0); cout.tie(0);

    int T = 1;
//  cin >> T;

    while (T--) {
        solve();
    }

    return 0;
}

E. Identical Parity

参考题解

K. Stack Sort

题意

给你 n 个数

把这 n 个数压入一些栈中，在依次弹出每个栈（弹完一个栈才能弹下一个栈）

问使弹出来的所有的数递增所需的最小栈数

解法

思维

由栈后进先出可知，若在压入一个数 x 时，若 x + 1 已被压入某个栈， 则 x 可入 x + 1 所在的栈，否则新开一个栈

代码

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
const int N = 5E4 + 10;

void solve() {
    int n;
    cin >> n;
    int ans = 0;
    set<int> st;
    for (int i = 0; i < n; ++ i) {
        int x;
        cin >> x;
        if (!st.count(x + 1)) ++ ans;
        st.insert(x);  
    }
    cout << ans << endl;

}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int T = 1;
    cin >> T;

    while (T --) {
        solve(); 
    } 

    return 0;
}

M. Best Carry Player

题意

给定 n 个数相加，算进位数

解法

高精度 / 模拟

代码

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
const int N = 5E4 + 10;

void solve() {
    int n;
    cin >> n;
    vector<int> arr;
    for (int i = 0; i < n; ++ i) {
        int x;
        cin >> x;
        arr.push_back(x);
    }

    int ans = 0;
    function<ll(ll a, ll b)> get = [&](ll a, ll b) -> ll{
        vector<int> abit, bbit;

        while (a) {
            abit.push_back(a % 10);
            a /= 10;
        }

        while (b) {
            bbit.push_back(b % 10);
            b /= 10;
        }
        vector<int> ret;
        int len = min((int)abit.size(), (int)bbit.size());
        int at = 0;
        int i = 0;
        for (i = 0; i < len; ++ i) {
            int t = abit[i] + bbit[i] + at;
            ans += at;
            at = 0;

            at = t / 10;
            ret.push_back(t % 10); 

        }

        while (i < (int)abit.size()) {
            int t = abit[i] + at;
            ans += at;
            at = 0;

            at = t / 10;
            ret.push_back(t % 10);
            ++ i;
        }

        while (i < (int)bbit.size()) {
            int t = bbit[i] + at;
            ans += at;
            at = 0;

            at = t / 10;
            ret.push_back(t % 10);
            ++ i;
        }

        while (at) {
            ans += at;
            ret.push_back(at % 10);
            at /= 10; 
        }

        ll tot = 0;
        while (ret.size()) {
            tot = tot * 10 + ret.back();
            ret.pop_back();
        }
        return tot;
    };

    ll tot = 0;
    for (int i = 0; i < n; ++ i) {
        tot = get(tot, arr[i]);
    }

    cout << ans << endl;

}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int T = 1;
    cin >> T;

    while (T --) {
        solve(); 
    } 

    return 0;
}
ICPCICPC 济南ICPC 西安The 2022 ICPC Asia Xian/Jinan Regional Contest算法竞赛题解
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
															
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																

							
							
						

															
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
前缀和与差分

							
							

							
快速排序模板

							
							

							
洛谷GESP C++上机题

							
							

							
YS-GPT

							
							

							
洛谷官方题单【算法1】

							
							

							
洛谷官方题单【入门】

							
							

							
数位DP

							
							

							
蓝桥杯-特殊时间

							
							

							
数学知识-常用算法模板

							
							

							
ModInt\mint  泛编程模板类